这算是我看的第一篇 ANNS 文章,感觉像是打开了新世界的大门,后续读了一些 ANNS 文章,感觉没有读这一篇那么心潮澎湃了。
# 论文动机
# 作者希望解决的问题
K 近邻检索(K-NNS)在很多场景有着很强的需求,naive 的思想就是扫一遍整个数据集,然后找到 KNN,但是这样做无疑是极大耗时间的。虽然后续有很多更好的 KNNS 算法提出,但是由于 curse of dimensionality 维度诅咒的存在 KNNS 只适用于低维度的数据。为了解决这一问题,KANNS 被提出,只是检索最近似的邻居。通过用召回率,即(检索得到的最近邻)/ K。
现有的很多算法,比如基于树的方法树检索算法,基于哈希的算法,基于 product quantization(PQ)的方法。但是基于临近图(proximity graph)的 ANNS 算法取得了更加出色的性能。
但是这些图算法有一些缺点:
1)查询步数呈现幂律分布。
2)有可能失去全局连通性,导致只在 cluster 进行查询。
# 作者提出的解决办法
作者根据 proximity graph 提出了 NSW。(NSW 我没有读)NSW 的核心就是通过贪心算法查询 p 节点的 M 个最近邻,然后把查到的 M 的最近邻作为 p 节点的邻居。
NSW 的查询复杂度是 ,因为平均查询步数为 ,而平均度数也为 。这就导致总的 distance 计算次数为平方。
而 HNSW 为了降低这个查询复杂度,提出了多层 graph 模型。

# HNSW 算法拆解
作者关于 HNSW 的介绍,HNSW 的结构实际上类似于跳表:
The Hierarchical NSW idea is also very similar to a well-known 1D probabilistic skip list structure [27] and can be described using its terms.
# 邻居选择策略
HNSW 其实是一个 DG+RNG 图。
DG 图就是下面这个每个三角形之内,不能有其他点,DG 图可以给 ANNS 提供很好的查询精度,但是对于高纬度数据,DG 图会退化为全连接,可以看这篇文章 DG 图:

RNG 图就是下面这个月牙里面不能有其他节点,if 𝑥 and 𝑦 are connected by edge 𝑒 ∈ 𝐸, then ∀𝑧 ∈ 𝑉 , with 𝛿 (𝑥, 𝑦) < 𝛿 (𝑥, 𝑧), or 𝛿 (𝑥, 𝑦) < 𝛿 (𝑧, 𝑦),这个 RNG 图我一开始很难理解,其实这个月牙是两个圆相交,那么这个月牙内每个节点到 x 或者 y 的距离一定是都要小于 x,y 的距离的。可以画个图,以 x 圆形以 xy 为半径和以 y 为圆形 xy 为半径进行画图相交得到月牙,那么这里面的所有节点到 x 和 y 的距离都小于 xy。

HNSW 借鉴了 RNG 的这种思想,也就是启发式选边,但是并没有构建一个真的 RNG 图,因为一个 RNG 的构建复杂度为 。
RNG 论文中对 RNG 图的定义:

其实就是指的月牙里面没有点。
so,首先我们 look one down 选边策略:

extendCandidates 是一个数据加强的策略,把 Candidate 的 neighbour 也加入到 Candidate 中,因为 KGraph 也提到过,邻居的邻居很有可能是邻居。
我们主要看这个核心的启发式选边策略:

extract nearest element from W to q ,也就是说这个循环是 distance 从小到大开始选边。这里的类 RNG 是,我们需要满足没有连接的边出现在上图说的月牙形状中,而不是说没有点出现在月牙中,这有点难理解。这个选边策略其实和 NSG 的选边策略相同。。。
RNG 图的要求,如果 x,y 要进行连接,那么不能出现一个节点到 x 或者 y 的距离都小于 x,y 的距离。而我们从小到大开始选边,那么默认满足了之前选择的节点到 q 的距离一定小于现在这个节点 e 到 q 的距离。那么如果出现之前选择的节点到 e 的距离小于 q 和 e 之间的距离,那么我们就触发了 RNG 的丢弃条件了。HNSW 叫启发式选边,而 NSG 叫 MRNG,难绷。。。
易远丁真,鉴定为最近邻。
这种启发式选边的最大好处就是继承了类似 RNG 的属性,就是是稀疏性。
作者说这样可以连接到不同的 cluster,其实这正是 RNG 的特性之一,RNG 的特定就是强连通性。因为如果节点出现聚集,那么两个 cluster 的边界节点很可能是稀疏的,也就是月牙状里面没有其他节点,那么我们就能够把他们进行连接。

# layer 搜索算法
首先是层检索算法,因为 HNSW 是一个分层的结构,所以我们检索时候实际上是从上到下进行检索,每一层都进行检索。

其实这就是一个贪心算法,换汤不换药。给定一个 Candidate list 和 result list,每一次迭代取出 Candidate 中和 q 最近的点 c,如果这个最近的点比 result 中离 q 最远的点 f 还要远,说明达到了局部最佳,这时候 break。如果还可以优化就继续检索 c 的邻居节点。
注意,贪心算法是非回溯的。在 NSG 中证明了 MRNG 是一个 MSNET,通过贪心非回溯算法得到的结果,它的搜索路径一定是单调路径。
# 插入算法
因为 HNSW 的多层结构,我们在插入的时候也是从上到下进行插入。

这个算法我觉得没有太多需要注意的地方。需要注意的就是,在选择 neighbour 之后需要加上双向边,这就导致了可能出现节点的度大于 。因此需要进行 shrink 操作。
插入法归纳步骤。1)随机 roll 一个层数 l,从当前图的 top level L 开始查询,每次就去最近邻,直到查到 l 层。2)使用贪心算法检索出候选邻居,并使用启发式算法对候选邻居进行选择,给这些邻居添加 双向边。3)如果邻居的度超过了 ,那么对邻居执行一次查询选择操作,并为候选邻居添加 单向边。
# 总的查询算法
第 0 层以上的,使用 ef=1,第 0 层使用用户指定的 ef。层次化查询,easy。

# 问题
如果设置固定层数,随机因子固定,对性能影响?
为什么通过启发式构建的图,能够使用贪婪算法?以及证明贪婪算法收敛?
# 构建参数影响
构建索引这里面有很多参数,比如 $M_{max0} \quad efConstruction \quad m_L\quad M $.
一般 选择为 。

作者也对 进行了研究,发现取 2M 时候效果最好
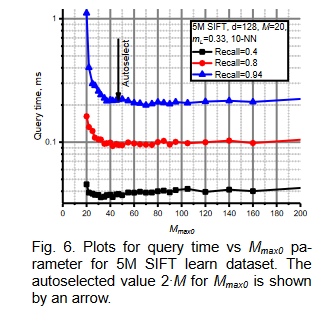
efconstruction 可以通过 simple data 来自动 configured。
唯一对用户有意义的参数就是 M,也就是节点的度,作者也对 M 的取值做了实验,12 或者 20 是一个比较好的选择,anns-benchmark 也是取 12 和 20:

# 性能评估
作者从四个方面对算法是性能进行评估:
# 和 baseline NSW 进行比较
使用维度为 4 的随机数据,可以看到 HNSW 吊打 NSW。

# 欧式空间内进行比较
用到的对比算法:


用到的数据集:
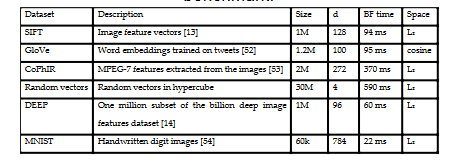
结果:

低纬度的随机数据,HNSW 略微好于 annoy,其他情况下都是吊打。
# 非欧空间
这个不是很懂,以后再看吧
# 和 pq 方法的对比
参数设置:

结果:

依旧是吊打,但是图方法的最大劣势就是耗内存很多。。。