论文阅读：FANNG

这篇文章就简单说一下 FANNG 这个算法（Fast Approximate Nearest Neighbour Graph）

# 本文贡献

# FANN 算法拆解

# 理想的图结构

首先看一下这个简单的贪心算法，这个算法让我思考的一个问题就是我们是否需要维持一个 visit 列表来保证非回溯，可以看到因为查询路径单调的原因，即使不维持 visit 列表，我们也能够不回头查询。所以 visit 列表最大的作用其实是当 Candidate 不是一个节点而是一组节点的时候，使用 visit 列表可以砍掉重复访问，因为我们的查询路径如果是单调的，即使 Candidate 是一组节点也不会发生回溯现象。

要使得这个查询算法在任意一个起始点都能找到查询点，那么我们需要保证， always an edge that leads to a vertex which is closer to the query. 这句话的翻译就是对于任意满足 $dis(Q,P_u) < dis(Q, P_v)$ 的节点 u，那么节点 u 一定能带领我们接近 p。因为所有节点必须满足至少（注意这个至少）有一条边能够使得查询更接近查询结果。好好回味这句话，这是精髓。这句话的意思实际上就是任意两点之间存在单调路径。（没错就是这样，任意两点之间存在单调路径就是至少有一条边能够 closer to query。这就是 MSNET 图。

因为只需要有一条边满足就行了，所以我们可以砍掉冗余边。这里我们定义，如果 p1 、 p2 这两个节点之间有边 $p_1 \rightarrow p_2$，那么对于任意的节点 p3 来说，如果满足 $ p2p3 < p1p3$ 那么我们说 p1p3 就是一条冗余边，p1p2 可以关闭 p1p3。因为我们满足了单调路径的条件，即 $\delta(p1,p3) > \delta(p2,p3)$，p1 到 p3 之间存在单调路径。但是如果$\delta(p1,p2) > \delta(p1,p3)$ ，那我们就发生了绕远路的情况，于是我们可以改变一下约束条件，只有 $\delta(p1,p3) > \delta(p2,p3) 并且\delta(p1,p2) < \delta(p1,p3)$，那么才将 p1,p2 视为冗余边：

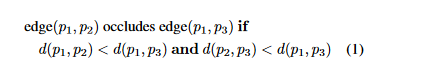
# 朴素构建

注意这里第一个标红的地方， sorted by distance(p_i, p_j) 。这一步 sort 很重要的，避免了之后添加上去的边需要 occlude 之前的边。

想了想这个所谓了关闭条件，我发现这玩意就是 RNG，它的选边策略和 NSG 以及 HNSW 不能说相似吧，只能说是一模一样。。。

让我们思考一个场景，我们需要判断一个节点 q 能不能被添加到 p 的邻居中，那么需要考虑之前所有在 result 列表中的节点 y，是否都满足 $dis(p, q) > dis(y, q)$。这 tm 不就是 HNSW 和 NSG 的选边策略一模一样吗？绕了半天，不说人话。。。。🖕 凸 (艹皿艹)

作者还煞有其事的说，通过某一条边关闭的边，那么两条边之间的的夹角至少是 60°，因此整个图就分散得很好。咋就是说呢，一整个无语住了。这不是 RNG 图推出的性质吗？

# 绝对最近邻保证

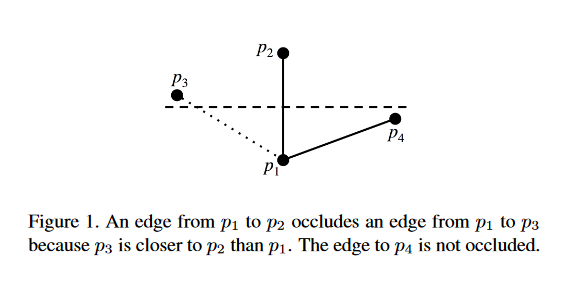
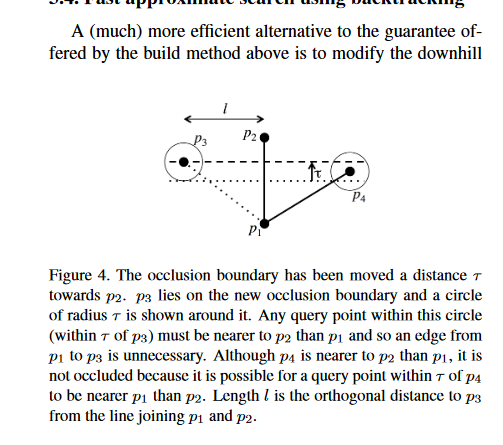
通过朴素算法 2 构建出的图，能够保证如果查询节点在图上，那么一定能够找到它的最近邻。但是需要查询不在图上 q 点的最近邻，作者给出了一个 relax 条件：

关闭边的条件得到了放松，但是我并没有搞明白这个操作是怎么做的。。。

# 回溯查询

这里说一下怎么把这个查询一个节点的算法改成 KANNS。就是把 n 改成一个大顶堆堆 W。

将第 11-12 行修改为：

$$if \quad dis(Q, P_u) < dis( Q, P_n) \quad or \quad |W| < size \quad then \\ W.add(P_u) \quad and \quad resize(W, size) \quad and \quad n =W.front()$$

这样的回溯方法说实话，效率挺低的，作者说可以传入一个参数 T，作用于 14 行，只选择 i<T 的边。

# 高效构建

没怎么看懂，不过感觉有点意义不大，还不如 search and select 呢。。。

# 实验结果

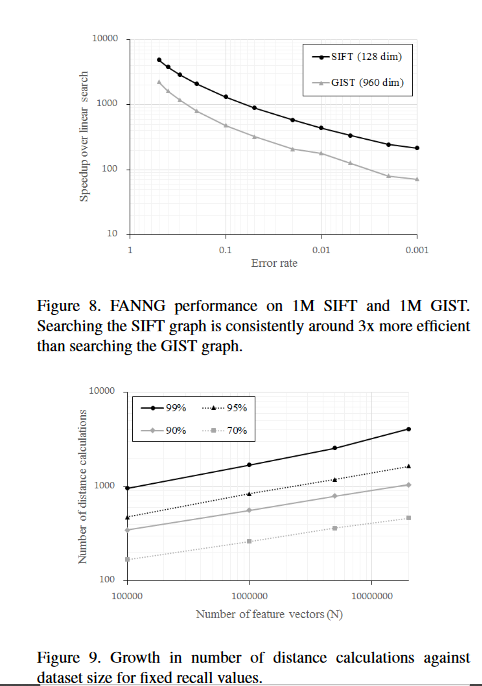
# 结论

这篇文章的思想还是很简单的，因为发表的时间最久，说实话收获不是很大。