最近邻检索树算法——KD树，Ball树,VP树 - 数据库

这篇文章主要聚焦一下各种奇奇怪怪的树查询算法。虽然我主要关注最近邻检索的图方法，但是因为很多图方法实际上都使用了各种 tree 作为辅助索引，所以有必要简单了解一下所有的树查询算法。

有请第一位 ~~受害者~~ 。

# KD 树

kd 树算是用的很广泛的一种最近邻检索树了，它的思想实际上和二叉搜索树很像。

看这张图就够了：

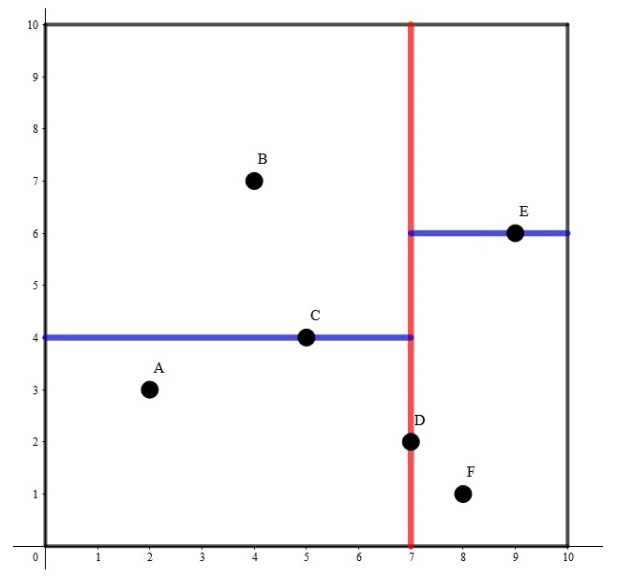
首先思考动机，为什么我们需要构建 KD 树？树结构是一种非常高效的数据结构，对于二叉搜索树，它的查询复杂度只有 h，也就是 log (n)。如果直接暴力检索最近邻，那么复杂度会是 n。

KD 树是什么？与搜索二叉树类似，通过比较数据，把大于当前节点的数据插入到树右侧，把小于节点的数据放到左侧。而 KD 树比较大小是在不同维度进行的。

例如，对于当前节点 root。我们比较所有数据点（p $\in E^d$ ) 在维度 0 的数据，对于某个向量 [1.1,3.4,...,0.1] 在 dim=0 的数据即 1.1，如果 1.1 小于 root（dim=0)，那么就把这个向量插入到左侧，如果小于就插入到右侧。同样在 KD 树下一层，我们比较 dim=1 的数据，按照同样方式进行插入。

一个很重要的优化方式就是，我们要保证 KD 树左右两边数据点数量差不多，这样进行插入时候可以保证得到的 KD 树尽可能平衡。于是我们构建 KD 树时候选择当前点集在当前维度下处于 中位数 的那个点作为 base，然后比较插入。

第二个优化的点，维度选择。我们尽量选择数据分布方差很大的维度。

所以构建方法：

假设我们已经知道了维空间内的个不同的点的坐标，要将其构建成一棵 k-D Tree，步骤如下：

若当前超长方体中只有一个点，返回这个点。
选择一个维度，将当前超长方体按照这个维度分成两个超长方体。
选择切割点：在方差大的维度上选择中位数那个点，这一维度上的值小于这个点的归入一个超长方体（左子树），其余的归入另一个超长方体（右子树）。
将选择的点作为这棵子树的根节点，递归对分出的两个超长方体构建左右子树，维护子树的信息。

这里定义可以参考：https://oi-wiki.org/ds/kdt/

代码实现我看的是：https://github.com/crvs/KDTree

构建树的算法：

	KDNodePtr KDTree::make_tree(const pointIndexArr::iterator &begin, //
	const pointIndexArr::iterator &end, //
	const size_t &length, //
	const size_t &level //
	) {
	if (begin == end) {
	return NewKDNodePtr(); // empty tree
	}

	size_t dim = begin->first.size();

	if (length > 1) {
	sort_on_idx(begin, end, level); // 类似于快排，就是把中位数放到正确的位置，同时左边的数都比他小，右边的数都比中位数大
	}

	auto middle = begin + (length / 2);

	auto l_begin = begin;
	auto l_end = middle;
	auto r_begin = middle + 1;
	auto r_end = end;

	size_t l_len = length / 2;
	size_t r_len = length - l_len - 1;

	KDNodePtr left;
	if (l_len > 0 && dim > 0) {
	left = make_tree(l_begin, l_end, l_len, (level + 1) % dim);
	} else {
	left = leaf;
	}
	KDNodePtr right;
	if (r_len > 0 && dim > 0) {
	right = make_tree(r_begin, r_end, r_len, (level + 1) % dim);
	} else {
	right = leaf;
	}

	// KDNode result = KDNode();
	return std::make_shared< KDNode >(*middle, left, right);
	}

他的代码没有用到第二个优化，选择划分的 dim 只是简单的递增取模。

查询算法：

	KDNodePtr KDTree::nearest_( //
	const KDNodePtr &branch, //
	const point_t &pt, //
	const size_t &level, //
	const KDNodePtr &best, //
	const double &best_dist //
	) {
	double d, dx, dx2;

	if (!bool(*branch)) { // 走到了一个叶子结点
	return NewKDNodePtr(); // basically, null
	}

	point_t branch_pt(*branch); // 之间重载了操作符 ()
	size_t dim = branch_pt.size();

	d = dist2(branch_pt, pt);
	dx = branch_pt.at(level) - pt.at(level);
	dx2 = dx * dx;

	KDNodePtr best_l = best;
	double best_dist_l = best_dist;

	if (d < best_dist) {
	best_dist_l = d;
	best_l = branch;
	}

	size_t next_lv = (level + 1) % dim;
	KDNodePtr section;
	KDNodePtr other;

	// select which branch makes sense to check
	if (dx > 0) {
	section = branch->left;
	other = branch->right;
	} else {
	section = branch->right;
	other = branch->left;
	}

	// keep nearest neighbor from further down the tree
	KDNodePtr further = nearest_(section, pt, next_lv, best_l, best_dist_l);
	if (!further->x.empty()) { //best_l 实际上是一个指针，这一步 check 并没有必要。
	double dl = dist2(further->x, pt);
	if (dl < best_dist_l) {
	best_dist_l = dl;
	best_l = further;
	}
	}
	// only check the other branch if it makes sense to do so
	if (dx2 < best_dist_l) { // 说明 other 这个 branch 也有可能能够找到最近邻
	further = nearest_(other, pt, next_lv, best_l, best_dist_l);
	if (!further->x.empty()) {
	double dl = dist2(further->x, pt);
	if (dl < best_dist_l) {
	best_dist_l = dl;
	best_l = further;
	}
	}
	}

	return best_l;
	};

查询的思想也和二叉树更类似，不多赘述。

# ball tree

ball tree 的思想更简单了。

将当前点集的质心作为 root，搜索离当前质心最远的节点 p，搜索离节点 p 最远的节点 q。通过 p，q 将当前点集进行划分为两个 cluster，看点离 p，q 哪个更近，如果离 p 更近就加入 p cluster，如果离 q 更近就加入 q cluster。反复迭代，知道到达最大深度。

首先取灰色的点作为 root，用 3 和 9 来划分两个 cluster。然后递归进行划分。

# VP treee

这里有一篇文章，对于我理解 VP tree 有很大帮助：http://stevehanov.ca/blog/?id=130

so，what is vp tree？

对于每一个节点 p，我们设置一个半径 r，把和该节点距离小于 r 的所有点插入到节点的左子树，把距离大于 r 的所有点插入到右子树。实际代码中，我们取点集中位数之前的所有点作为左子树，中位数之后的点作为右子树。

查询时候，需要去确定向左还是向右去查询。

如果查询的点 x 在当前也就是距离小于 tau，把当前 p 加入到 result 中（因为需要查 k 个最近邻）， tau 始终等于结果 result 中距离 x 的最大距离。

因为 x 在圆内，于是我们向左子树进行查询，蓝色的点，就是我们在左子树中查询得到的点，并且更新得到了 tau。

如果 tau > distance to shell，说明外部还可能有节点，需要向右子树进行查询。

	#include <stdlib.h>
	#include <algorithm>
	#include <vector>
	#include <stdio.h>
	#include <queue>
	#include <limits>

	template<typename T, double (*distance)( const T&, const T& )>
	class VpTree
	{
	public:
	VpTree() : _root(0) {}

	~VpTree() {
	delete _root;
	}

	void create( const std::vector& items ) {
	delete _root;
	_items = items;
	_root = buildFromPoints(0, items.size());
	}

	void search( const T& target, int k, std::vector* results,
	std::vector<double>* distances)
	{
	std::priority_queue<HeapItem> heap;

	_tau = std::numeric_limits::max();
	search( _root, target, k, heap );

	results->clear(); distances->clear();

	while( !heap.empty() ) {
	results->push_back( _items[heap.top().index] );
	distances->push_back( heap.top().dist );
	heap.pop();
	}

	std::reverse( results->begin(), results->end() );
	std::reverse( distances->begin(), distances->end() );
	}

	private:
	std::vector<T> _items;
	double _tau;

	struct Node
	{
	int index;
	double threshold;
	Node* left;
	Node* right;

	Node() :
	index(0), threshold(0.), left(0), right(0) {}

	~Node() {
	delete left;
	delete right;
	}
	}* _root;

	struct HeapItem {
	HeapItem( int index, double dist) :
	index(index), dist(dist) {}
	int index;
	double dist;
	bool operator<( const HeapItem& o ) const {
	return dist < o.dist;
	}
	};

	struct DistanceComparator
	{
	const T& item;
	DistanceComparator( const T& item ) : item(item) {}
	bool operator()(const T& a, const T& b) {
	return distance( item, a ) < distance( item, b );
	}
	};

	Node* buildFromPoints( int lower, int upper )
	{
	if ( upper == lower ) {
	return NULL;
	}

	Node* node = new Node();
	node->index = lower;

	if ( upper - lower > 1 ) {

	// choose an arbitrary point and move it to the start
	int i = (int)((double)rand() / RAND_MAX * (upper - lower - 1) ) + lower;
	std::swap( _items[lower], _items[i] );

	int median = ( upper + lower ) / 2;

	// partitian around the median distance
	std::nth_element(
	_items.begin() + lower + 1,
	_items.begin() + median,
	_items.begin() + upper,
	DistanceComparator( _items[lower] ));

	// what was the median?
	node->threshold = distance( _items[lower], _items[median] );

	node->index = lower;
	node->left = buildFromPoints( lower + 1, median );
	node->right = buildFromPoints( median, upper );
	}

	return node;
	}

	void search( Node* node, const T& target, int k,
	std::priority_queue& heap )
	{
	if ( node == NULL ) return;

	double dist = distance( _items[node->index], target );
	//printf("dist=%g tau=%gn", dist, _tau );

	if ( dist < _tau ) {
	if ( heap.size() == k ) heap.pop();
	heap.push( HeapItem(node->index, dist) );
	if ( heap.size() == k ) _tau = heap.top().dist;
	}


	if ( node->left == NULL && node->right == NULL ) {
	return;
	}

	if ( dist < node->threshold ) {
	search( node->left, target, k, heap );
	if ( dist + _tau >= node->threshold ) { // 说明外部还有可能有节点。
	search( node->right, target, k, heap );
	}

	} else {
	search( node->right, target, k, heap );
	if ( dist - _tau <= node->threshold ) {
	search( node->left, target, k, heap );
	}
	}
	}
	};

# Brute Force

说白了就是暴力检索。

ANNS

# KD 树

# ball tree

# VP treee

# Brute Force

论文阅读：FANNG

cpp奇淫巧技