# PageRank
在理解 pagerank 算法之前需要理解 Markov chain。可以说 PageRank 的核心就是 Markov 算法,PageRank 的执行过程、收敛条件都可以从 Markov 中得到答案。
# Markov chain
# 基本定义
马尔科夫性:未来只依赖现在(假设现在已知),而与过去无关。
一阶马尔科夫链:
其中 $P (X_t| X_0,X_1,\cdots ,X_{t-1}) $ ,表示在 $X_0,X_1,\cdots ,X_{t-1} X_t P (X_t| X_{t-1})$ 相等,说明 的概率只由 决定。这就是未来只依赖现在(假设现在已知),而与过去无关。
n 阶马尔科夫链:
# 转移矩阵
马尔科夫链在 t-1 时刻处于 j 状态,那么时刻 t 转移到 i 状态的概率可以记作:
马尔科夫链的转移概率就可以用转移矩阵表示为 P。
马尔科夫链在 t 时刻的状态分布可以记作
表示 t 时刻处于 i 状态的概率。
这块如果有疑虑可以查阅资料。
# 平稳分布
此时 $\pi $ 就是平稳分布。意思是,状态向量 无法再通过状态转移 P,到达新的状态分布,则表示马尔科夫链已经到达收敛。
不可约、非周期且正常返的马尔科夫链有唯一的平稳分布
# PageRank 算法
# PageRank 定义
传统的 web 结构中,都是通过网页之间互联(可以看做有向图)来实现访问。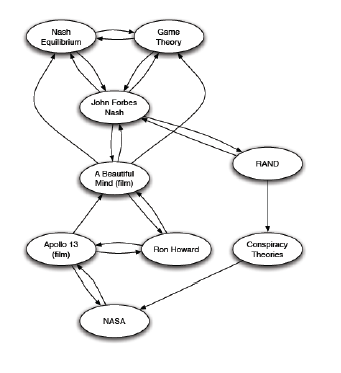
如图所示,我们如何表示某个网页 s 的重要性呢?看有多少网页指向这个 s 网页。这个很好理解,那么重要的网页指向的网页肯定也是比较重要的。于是我们有了两个基本的关于网页 page 重要性的定义:
- 被很多网页指向的那个网页,它的重要性一定很高。
- 被很重要的网页指向的网页,那么它的重要性也应该高。
# PageRank 算法的执行过程
# 初始化
我们先对每个 graph 节点的 rank 值做初始化,可以定义初始的分布向量
n 表示 graph 节点的总数,我们预定义所有节点的 rank 值相加要为 1,且初始相等。
# 迭代
做随机游走
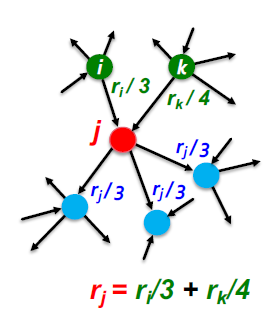
定义
整个过程可以写为:
M 是转移矩阵,如果 i、j 两个节点有边相连,那么 Mij 表示由 j 转移到 i 的概率,值就是 1/dj。dj 是节点 j 的出度
# 收敛
这是一个马尔科夫过程,最终会达到一个平稳分布,也就是收敛。
实际执行时,只需要满足
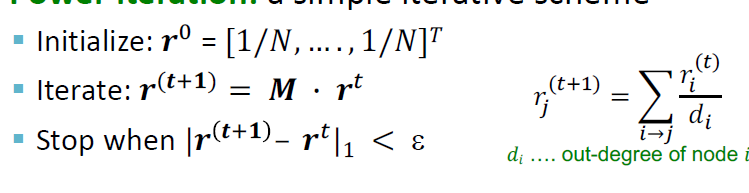
# PageRank 算法的一般定义
# 问题
Spider trap
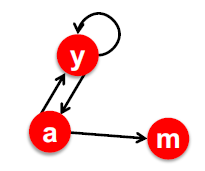
如果某个节点只有一条出边,且这条出边指向它自己。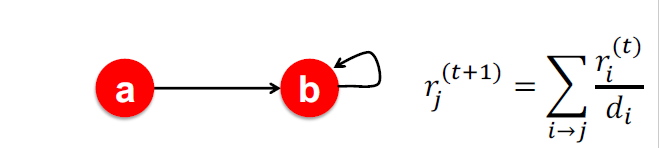
那么最终该节点会吃掉所有节点的 rank 值。很好理解,如果 j 是这种节点,那么转移矩阵 M 的第 j 列只有 Mjj 为 1,其余值。每次 迭代时候,其他节点就吃不到 j 节点的 rank 值,因为它不转出,而 j 节点会一直吃到其他节点的 rank 值,因为存在 。
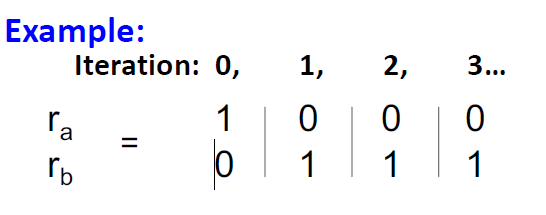
Dead Ends
同理节点 j 没有出边,只有入边:
对应的转移矩阵 M 中第 j 列全为 0,那么每次迭代 时,没有任何一个节点(包括 j 节点自己)能吃到 j 的值。而其他节点还在给 j 节点输送 rank 值。
于是,每次迭代时候,
# 一般化

定义一个转移系数,每次有 的可能性跳转到其他节点
以 dead end 为例子,假设 j 为 dead end。虽然刚开始也会有 rank 值的损失,但随着迭代的进行,只要满足下列式子就不会有 rank 值的减小。
随着迭代的进行,sum (r) 减小的幅度会逐渐变为 0。也就是说,一般化的 PageRank 算法也是可以收敛的。
假设转移矩阵为:

初始的 r 为
经历了 100 次迭代后,loss sum:
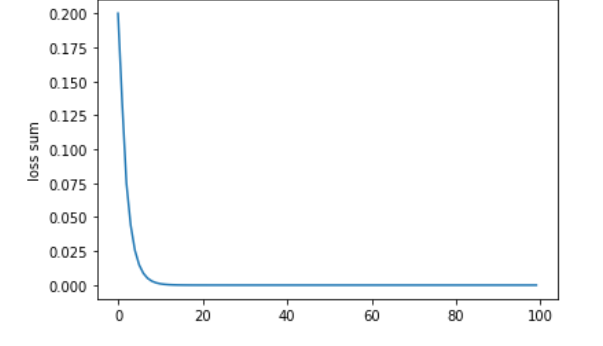
# Personalized PageRank
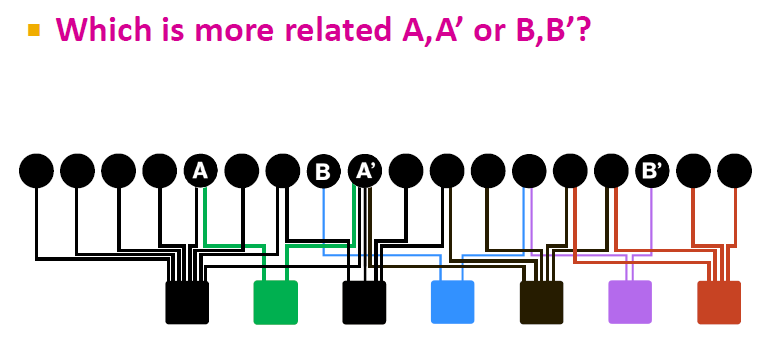
提出的问题就是怎么寻找两个节点之间的关联性。
比如对于节点 Q,如何查询和他最相似的节点?
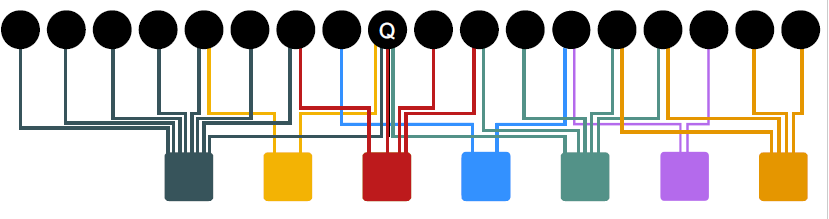
# 执行过程
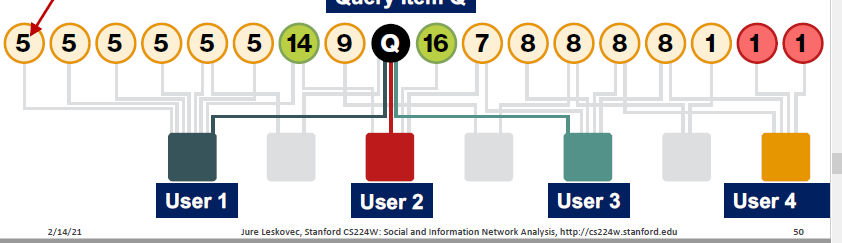
Q 连接到 user1,2,3。而不同的 user 对于 Q 的节点不一样,这就是一个转移概率
sum(s)=1
这个就是 Q 跳转到 user 的概率。
假设 Q 根据 weight 跳转到 User1,那么执行 random walk,随机跳转到其他的节点,每次访问了某个节点就将该节点的 count+1。同时进行随机 reset,重新回到节点 Q,再一次进行上述过程。
算法执行过程:

统计最后哪个节点 count 数最多,就表示和节点 Q 最相似。
# matrix factorization
这一块不怎么熟悉,有待进一步学习。