HetGNN：算法简单分析

# 总览

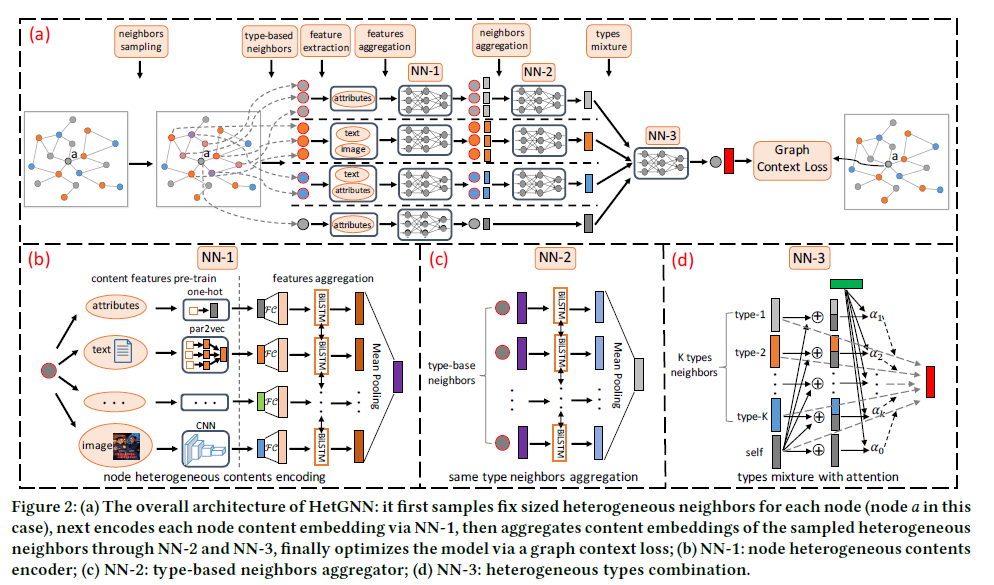
这个算法主要分为 3 个步骤：

# Sampling Heterogeneous Neighbors

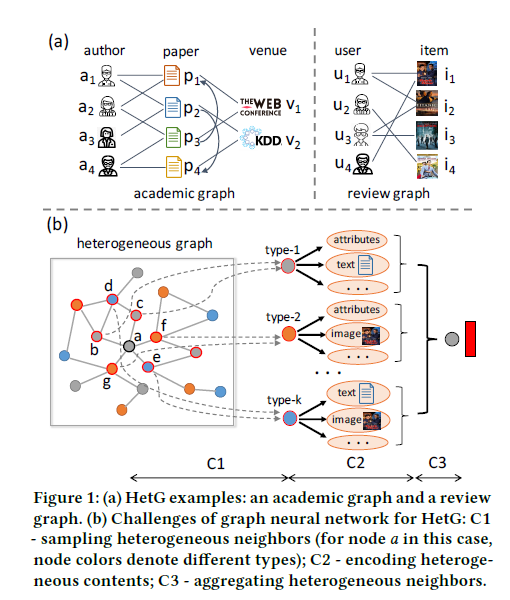
第一步采样得到邻居节点，作者的做法就是 random walk with restart（RWR）。这个 RWR 过程直接在异构图上进行，所以它会采样到各种节点，当节点数达到了设定的固定节点数，就停止采样。

第二步，Group nodes。就把采样得到的不同节点 group，选取每个类别下 topk 频率的节点作为邻居节点。

# Encoding Heterogeneous Contents

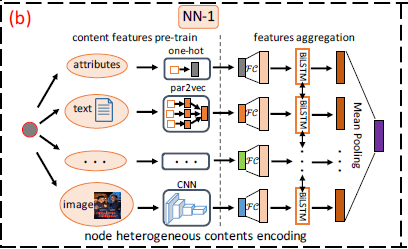
因为异构图上不同节点的 content 不同，有的节点可能是 text，有的可能是 image，有个节点既有 image 也有 text。这一步做的就是把这些 content 提取出来，并输出一个 d 维的向量。

$$f_{1}(v)=\frac{\sum_{i \in C_{v}}\left[\overrightarrow{L S T M}\left\{\mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)\right\} \bigoplus \overleftarrow{L S T M}\left\{\mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)\right\}\right]}{\left|C_{v}\right|}$$

其中$x_i$ 值得是原始的 content，FC 是变换函数，这个 FC 可以是 CNN 可以是 RNN，反正就是将原本的 content 转换为向量。

LSTM 结构：

$$\begin{aligned} &\mathrm{z}_{i}=\sigma\left(\mathcal{U}_{z} \mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)+\mathcal{W}_{z} \mathrm{~h}_{i-1}+\mathrm{b}_{z}\right) \\ &\mathrm{f}_{i}=\sigma\left(\mathcal{U}_{f} \mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)+\mathcal{W}_{f} \mathrm{~h}_{i-1}+\mathrm{b}_{f}\right) \\ &\mathrm{o}_{i}=\sigma\left(\mathcal{U}_{o} \mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)+\mathcal{W}_{o} \mathrm{~h}_{i-1}+\mathrm{b}_{o}\right) \\ &\hat{\mathrm{c}}_{i}=\tanh \left(\mathcal{U}_{c} \mathcal{F} C_{\theta_{x}}\left(\mathrm{x}_{i}\right)+\mathcal{W}_{c} \mathrm{~h}_{i-1}+\mathrm{b}_{c}\right) \\ &\mathrm{c}_{i}=\mathrm{f}_{i} \circ \mathrm{c}_{i-1}+\mathrm{z}_{i} \circ \hat{\mathrm{c}}_{i} \\ &\mathrm{~h}_{i}=\tanh \left(\mathrm{c}_{i}\right) \circ \mathrm{o}_{i} \end{aligned}$$

通过双向 LSTM 把 content 聚合起来，注意这一步的聚合是只聚合了 content，也就说是在单个节点上做的。

最后通过 mean pooling 输出一个 d 维向量。

# Aggregating Heterogeneous Neighbors

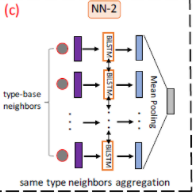
第一步就是基于相同 type 的 neighbor 聚合：

同样使用一个 LSTM 进行聚合。

$$f_{2}^{t}(v)=\frac{\sum_{v^{\prime} \in N_{t}(v)}\left[\overrightarrow{L S T M}\left\{f_{1}\left(v^{\prime}\right)\right\} \bigoplus \overleftarrow{L S T M}\left\{f_{1}\left(v^{\prime}\right)\right\}\right]}{\left|N_{t}(v)\right|}$$

Using different Bi-LSTMs to distinguish different node types for neighbors aggregation.

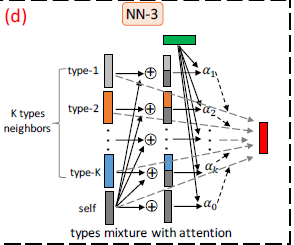
第二步，聚合不同 type 的 neighbor 信息：

不同的 embedding 对于节点的作用不同，其中$f_1(v)$ 是节点 v 经过 encoder 阶段产生的向量。其中$\mathcal{F}(v)=\left\{f_{1}(v) \cup\left(f_{2}^{t}(v), t \in O_{V}\right)\right.$：

$$\begin{gathered} \mathcal{E}_{v}=\sum_{f_{i} \in \mathcal{F}(v)} \alpha^{v, i} f_{i} \\ \alpha^{v, i}=\frac{\exp \left\{L e a k y \operatorname{ReLU}\left(u^{T}\left[f_{i} \bigoplus f_{1}(v)\right]\right)\right\}}{\left.\sum_{f_{j} \in \mathcal{F}(v)} \exp \left\{\operatorname{LeakyReLU(u^{T}}\left[f_{j} \oplus f_{1}(v)\right]\right)\right\}} \end{gathered}$$