# 训练图神经网络
# 节点分类
# 网络模型
# 构建一个 2 层的 GNN 模型 | |
import dgl.nn as dglnn | |
import torch.nn as nn | |
import torch | |
import dgl | |
import torch.nn.functional as F | |
class SAGE(nn.Module): | |
def __init__(self, in_feats, hid_feats, out_feats): | |
super().__init__() | |
# 实例化 SAGEConve,in_feats 是输入特征的维度,out_feats 是输出特征的维度,aggregator_type 是聚合函数的类型 | |
self.conv1 = dglnn.SAGEConv( | |
in_feats=in_feats, out_feats=hid_feats, aggregator_type='mean') | |
self.conv2 = dglnn.SAGEConv( | |
in_feats=hid_feats, out_feats=out_feats, aggregator_type='mean') | |
def forward(self, graph, inputs): | |
# 输入是节点的特征 | |
h = self.conv1(graph, inputs) | |
h = F.relu(h) | |
h = self.conv2(graph, h) | |
return h |
# 导入数据
graph = CiteseerGraphDataset()[0] | |
graph = graph.to('cuda') # 放到 cuda 上进行训练 |
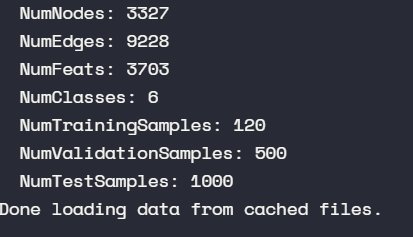

可以看到只是用了 120 个训练节点。
# 处理 mask
node_features = graph.ndata['feat'] | |
node_labels = graph.ndata['label'] | |
train_mask = graph.ndata['train_mask'] | |
valid_mask = graph.ndata['val_mask'] | |
test_mask = graph.ndata['test_mask'] | |
n_features = node_features.shape[1] | |
n_labels = int(node_labels.max().item() + 1) |
# 评估函数
def evaluate(model, graph, features, labels, mask): | |
model.eval() | |
with torch.no_grad(): | |
logits = model(graph, features) | |
logits = logits[mask] | |
labels = labels[mask] | |
_, indices = torch.max(logits, dim=1) | |
correct = torch.sum(indices == labels) | |
return correct.item() * 1.0 / len(labels) |
# 训练过程
model = SAGE(in_feats=n_features, hid_feats=100, out_feats=n_labels) | |
model = model.to('cuda') | |
opt = torch.optim.Adam(model.parameters()) | |
for epoch in range(1000): | |
model.train() | |
# 使用所有节点 (全图) 进行前向传播计算 | |
logits = model(graph, node_features) | |
# 计算损失值 | |
loss = F.cross_entropy(logits[train_mask], node_labels[train_mask]) | |
# 计算验证集的准确度 | |
acc = evaluate(model, graph, node_features, node_labels, valid_mask) | |
# 进行反向传播计算 | |
opt.zero_grad() | |
loss.backward() | |
opt.step() | |
acc = evaluate(model, graph, node_features, node_labels, test_mask) | |
acc |
0.668
可以看到只用了 120 个节点,但却最后的准确率达到了 0.668
# 异构图上的节点分类
# Define a Heterograph Conv model | |
class RGCN(nn.Module): | |
def __init__(self, in_feats, hid_feats, out_feats, rel_names): | |
super().__init__() | |
# 实例化 HeteroGraphConv,in_feats 是输入特征的维度,out_feats 是输出特征的维度,aggregate 是聚合函数的类型 | |
self.conv1 = dglnn.HeteroGraphConv({ | |
rel: dglnn.GraphConv(in_feats, hid_feats) | |
for rel in rel_names}, aggregate='sum') | |
self.conv2 = dglnn.HeteroGraphConv({ | |
rel: dglnn.GraphConv(hid_feats, out_feats) | |
for rel in rel_names}, aggregate='sum') | |
def forward(self, graph, inputs): | |
# 输入是节点的特征字典 | |
h = self.conv1(graph, inputs) | |
h = {k: F.relu(v) for k, v in h.items()} | |
h = self.conv2(graph, h) | |
return h | |
model = RGCN(n_hetero_features, 20, n_user_classes, hetero_graph.etypes) | |
user_feats = hetero_graph.nodes['user'].data['feature'] | |
item_feats = hetero_graph.nodes['item'].data['feature'] | |
labels = hetero_graph.nodes['user'].data['label'] | |
train_mask = hetero_graph.nodes['user'].data['train_mask'] | |
node_features = {'user': user_feats, 'item': item_feats} | |
h_dict = model(hetero_graph, {'user': user_feats, 'item': item_feats}) | |
h_user = h_dict['user'] | |
h_item = h_dict['item'] | |
opt = torch.optim.Adam(model.parameters()) | |
# 只对 user 节点进行预测 | |
for epoch in range(5): | |
model.train() | |
# 使用所有节点的特征进行前向传播计算,并提取输出的 user 节点嵌入 | |
logits = model(hetero_graph, node_features)['user'] | |
# 计算损失值 | |
loss = F.cross_entropy(logits[train_mask], labels[train_mask]) | |
# 计算验证集的准确度。在本例中省略。 | |
# 进行反向传播计算 | |
opt.zero_grad() | |
loss.backward() | |
opt.step() | |
print(loss.item()) | |
# 如果需要的话,保存训练好的模型。本例中省略。 |
大同小异,感觉,后面慢慢看吧。