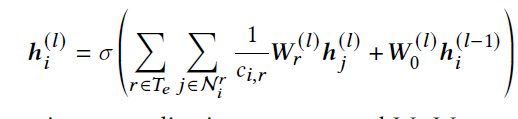读后感：Are we really making much progress? Revisiting, benchmarking, and refining heterogeneous graph neural networks(详解)

# 读后感

最近被师兄推荐了一篇异构图综述性质的文章。感觉看了之后挺有收获的，就把自己的理解写下来。

# 论文核心思想

GAT 等基于同构图的算法应用在异构图上未必比应用在那些为异构图设计的算法要差。

# 论文贡献

• 系统性地整合了现有的异构图算法的效果。
• 提出了 HGB（异构图的 benchmark）
• 提出了 simple-HGN 模型

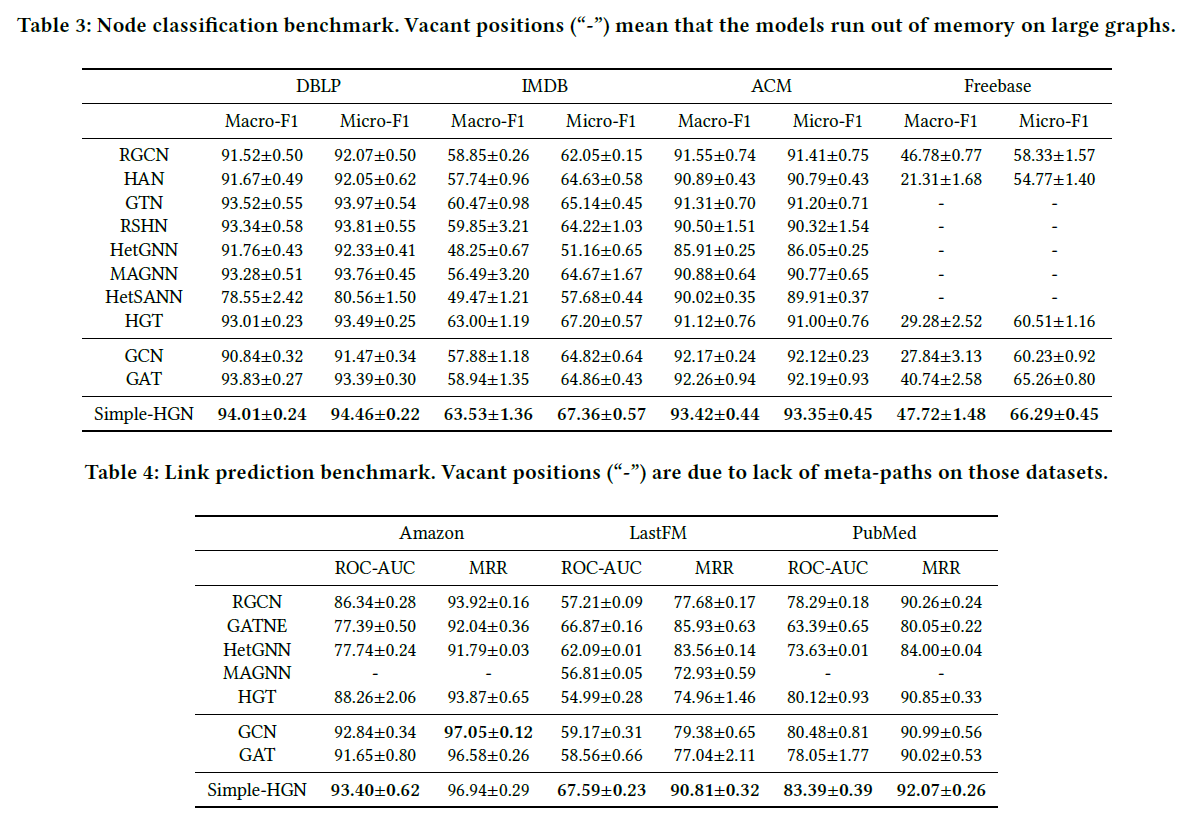
# 以前的模型

# node classification

• HAN （这个之前复现过效果还行）

• GTN Graph transformer network
• RSHN Relation structure-aware heterogeneous graph neural network
• HetGNN heterogeneous graph neural network（这个算法还是很优秀的，感觉，思路很清楚）
• MAGNN meta-path aggregate graph neural network，HAN 的加强版。
• HGT heterogeneous graph transformer
• HetSANN Attention-based graph neural network for heterogeneous structural learning (这个算法细节没有给出）

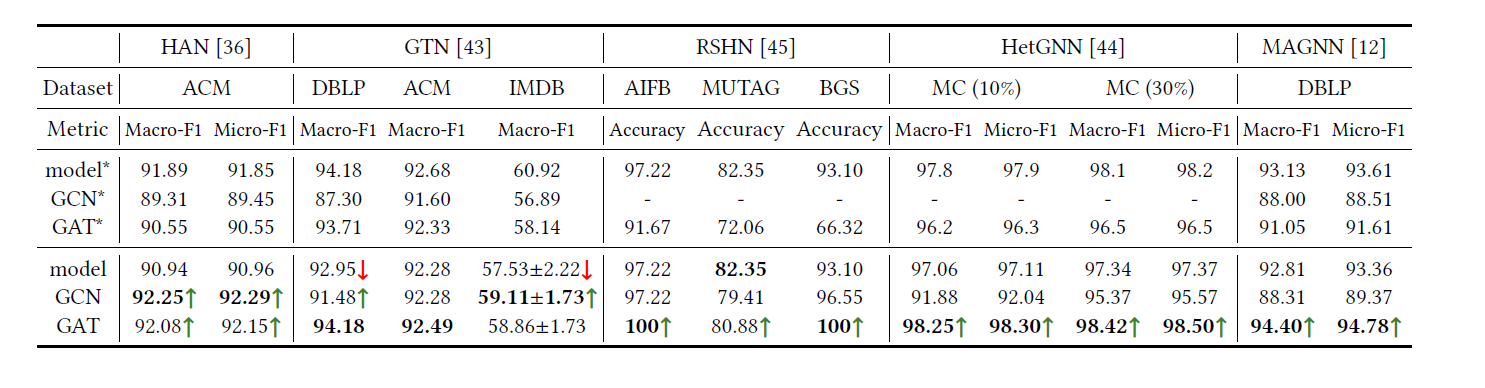
# Link Prediction

• RGCN 简单的异构图消息传递模型

• GATNE General attributed multiplex heterogeneous network embedding

# Knowledge-Aware Recommendation

• KGCN、KGNN-LS
• KGAT

# 这些模型存在的问题

这些模型都或多或少有些问题，一个常见的问题就是‘information missing in homogeneous baselines’ 。就之前看的 HAN 为例子，HAN 使用了 Metapath 将异构图提取为同构图。但 GAT 作为 baseline 只作用在了一个 Metapath 提取的 subgraph 上。

# Dataset

# node classification

# Link Prediction

# Knowledge-Aware Recommendation

# pipeline

这是论文中给出的 pipeline 的示意图，主要分为三个步骤 Feature Preprocessing、HGNN、Downstream Decorders。

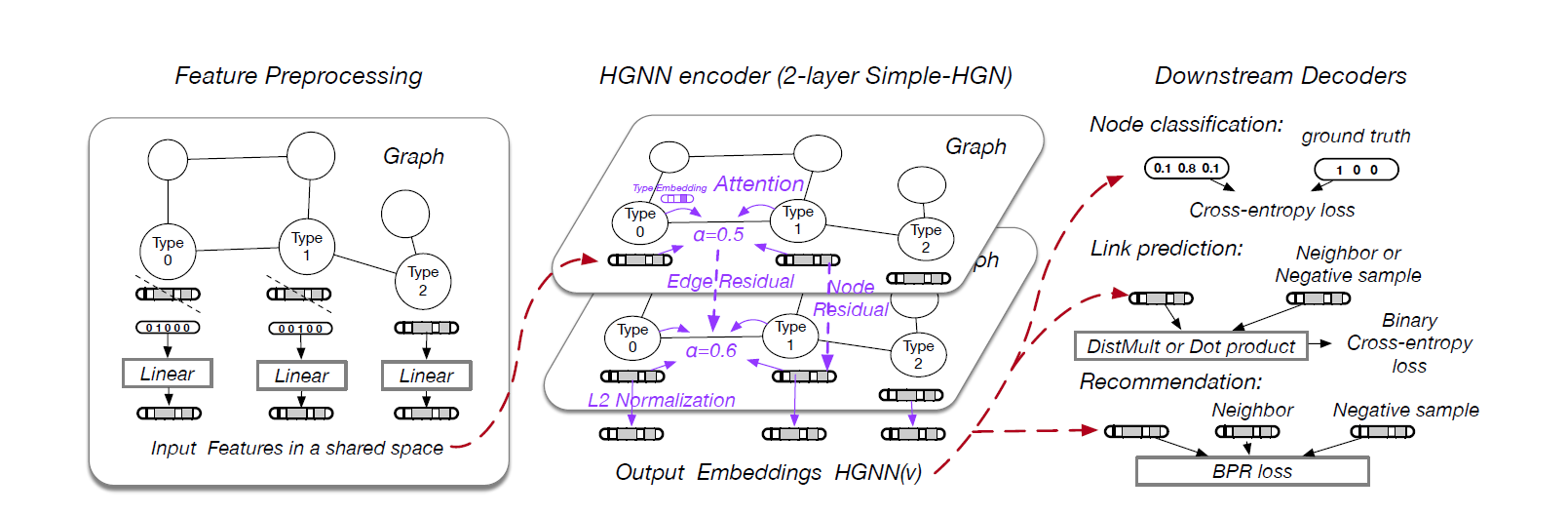
# Feature Preprocessing

# Linear Transformation

特征映射相同维度：project feature of different types of nodes to a share vec space.

# Useful Types Selection

选择有用的 type 节点。这里作者的做法是保留特定 type 节点的特征，将其他 type 节点特征全用 one-hot 代替。

# Downstream Decoders and Loss function

说白了就是根据下游任务选择 decoder，对于 Node Classification 那么就是选择交叉熵。

# A SIMPLE HETEROGENEOUS GNN

这里简单说一下这个模型，论文里还是说的很清楚的。

# Learnable Edge-type Embedding

模型每一层给每一种边类型分配一个可学习的 embedding。

attention 系数：

$$\hat{\alpha}_{i j}=\frac{\exp \left(\operatorname{LeakyReLU}\left(a^{T}\left[W h_{i}\left\|W h_{j}\right\| W_{r} r_{\psi(\langle i, j\rangle)}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\operatorname{LeakyReLU}\left(a^{T}\left[W h_{i}\left\|W h_{k}\right\| W_{r} r_{\psi}(\langle i, k\rangle)\right]\right)\right)}$$

其中$r_{\psi(\langle i, j\rangle)}$ 就是边 $\psi(\langle i, j\rangle)$ 的 embedding。这个$W_r$ 也是一个可学习的参数。

# Residual Connection

# Node Residual

这里的 node residual 还是简单的，就是原本的 residual 方法加入个$W_{ses}^{(l)}$ 可学习参数。

$$\boldsymbol{h}_{i}^{(l)}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{(l)} W^{(l)} \boldsymbol{h}_{j}^{(l-1)}+\boldsymbol{h}_{i}^{(l-1)}\right)$$

$$\boldsymbol{h}_{i}^{(l)}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{(l)} W^{(l)} \boldsymbol{h}_{j}^{(l-1)}+W_{\mathrm{res}}^{(l)} \boldsymbol{h}_{i}^{(l-1)}\right)$$

# Edge Residual

$$\begin{gathered} \alpha_{i j k}^{(l)}=(1-\beta) \hat{\alpha}_{i j k}^{(l)}+\beta \alpha_{i j k}^{(l-1)} \\ \hat{h}_{i k}^{(l)}=\sum_{j \in \mathcal{N}_{i}} \alpha_{i j k}^{(l)} W_{k}^{(l)} h_{j}^{(l-1)} \\ h_{i}^{(l)}=\sigma\left(\prod_{k=1}^{K} \hat{h}_{i k}^{(l)}+W_{\operatorname{res}(k)}^{(l)} h_{i}^{(l-1)}\right) \end{gathered}$$

说白了就是 attention 加了个动量，这个 $\beta$ 是一个超参数。

# Adaptation for Link Prediction.

We slightly modify the model architecture for better performance on link prediction. Edge residual is removed and the final embedding is the concatenation of embeddings from all the layers. This adapted version is similar to JKNet.

# L2 Norm

在 output 层加上一个 L2 norm

$$o_{i}=\frac{\boldsymbol{h}_{i}^{(L)}}{\left\|\boldsymbol{h}_{i}^{(L)}\right\|}$$

# benchmark